Краткие сведения по геометрии

Категория:
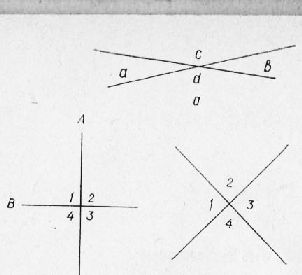
Технические чертежи


Краткие сведения по геометрии

Как известно из геометрии, линии бывают прямые и кривые. Прямые линии разделяются на вертикальные, горизонтальные и наклон-н ы е. При пересечении двух прямых линий образуются четыре угла а, Ь, с, d (рис. 5, а). Углы а и b равны между собой и меньше углов end, которые тоже равны между собой; первые из них называются острыми углами (меньше 90°), вторые — тупыми (больше 90°). Когда при пересечении двух прямых линий все четыре угла получаются равными, например, углы 1, 2, 3, 4 (рис. 5, б), тогда они носят название прямых углов (90°). Линии, образующие угол, называются сторонами угла, а точка, в которой стороны сходятся, — вершиной угла. Величина угла зависит только от наклона сторон, но не от их длины.

Линии, образующие при пересечении друг с другом прямые углы, называются взаимно перпендикулярными, или перпендикулярами.

Если приложить к поверхности стола линейку несколько раз и в разных направлениях и если все точки линейки совпадут с поверхностью стола (если, конечно, линейка правильно выстрогана по прямой линии), то такая поверхность называется плоскостью.

Рис. 1. Пересечение двух линий: а — прямых; б — перпендикулярных.

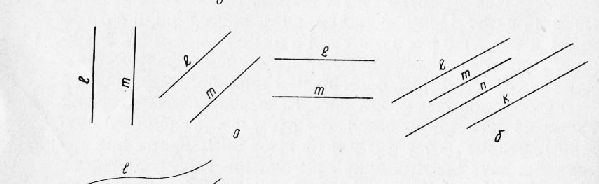
Рис. 2. Параллельные линии.

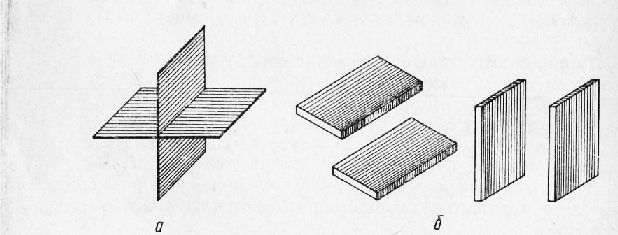
Рис. 3. Плоскости: а — взаимно перпендикулярные; б — параллельные.

Все сказанное о параллельных и перпендикулярных линиях в одинаковой мере относится также и к плоскостям. Так, две плоскости, при продолжении пересекающиеся друг с другом под прямым углом, называются взаимно перпендикулярными (рис. 3, а).

Плоскости, которые при продолжении не пересекаются, называются параллельными (рис. 3, б).

Часть плоскости или поверхности, ограниченная со всех сторон отрезками линий — прямых, кривых или тех и других вместе, называется геометрической фигурой.

Фигура, состоящая из трех замкнутых отрезков прямой, называется треугольником. Если отрезки разные, то треугольник называется разносторонним; если все отрезки равны между собой, то треугольник называется равносторонним; если только две стороны равны между собой, а третья меньше или больше одной из двух равных, то он называется равнобедренным; и, наконец, когда в треугольнике один угол прямой, т. е. 90°, то треугольник называется прямоугольным.

Фигура, состоящая из четырех замкнутых отрезков прямой, называется четырехугольником. Если все стороны равны и углы прямые, то четырехугольник называется квадратом. Четырехугольник, у которого равны все стороны и противоположные углы, называется ромбом. Четырехугольник, у которого противоположные стороны равны и все углы прямые, называется прямоугольником. Если в четырехугольнике противоположные стороны попарно равны и углы не прямые, то он называется параллелограммом. Если в четырехугольнике две стороны параллельны, а две другие не параллельны, то он называется трапецией.

В зависимости от числа сторон фигуры бывают пятиугольниками, шестиугольниками, семиугольниками и т. д. Их принято называть многоугольниками.

Рис. 4. Треугольники. а — разносторонний; б — равносторонний; в — равнобедренный; г, д — прямоугольные.

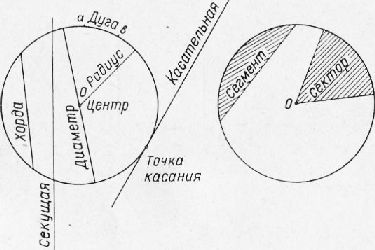
Многоугольник, состоящий из пяти равных сторон, называется правильным пятиугольником и т. д.; если же стороны или одна из них не равны другим, тогда он называется неправильным пятиугольником.

Замкнутая кривая линия на плоскости, все точки которой находятся на одинаковом расстоянии от одной точки (О), называется окружностью, а точка О — центром данной окружности. Плоскость, ограниченная окружностью, называется кругом (круг — это плоскость, а окружность — линия). Часть линии, например а — Ь, называется дугой. Прямая, соединяющая две точки окружности, но не проходящая через центр О, называется хордой. Прямая, соединяющая две точки окружности и проходящая через центр О, называется диаметром. Прямая, соединяющая точку окружности с центром О, называется радиусом, который в два раза короче диаметра. Прямая, пересекающая окружность, называется секущей; прямая, имеющая с окружностью лишь одну общую точку, называется касательнойк этой окружности, а сама точка — точкой касания.

Часть круга, ограниченная двумя радиусами и дугой, называется сектором, а ограниченная хордой и дугой,— сегментом. Окружность делится на 360 равных частей. Каждая такая часть окружности называется дуговым градусом. Два радиуса, соединяющие центр с концами одного дугового градуса, образуют один угловой градус.

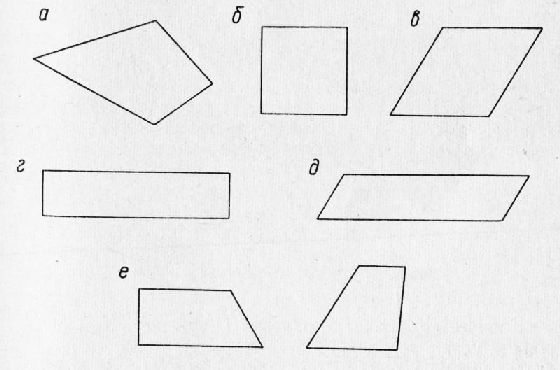
Рис. 5. Четырехугольники: а — четырехугольник; б — квадрат; в — ромб; г — прямоугольник; д — параллелограмм; е — трапеции.

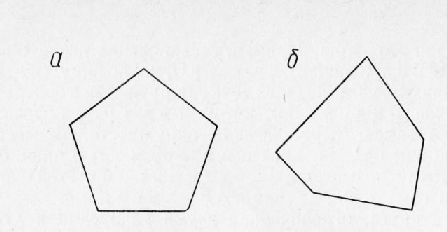
Рис. 6. Пятиугольники: а — правильный; б — неправильный.

Рис. 7. Элементы окружности и круга.

Количество дуговых градусов окружности между сторонами утла с вершиной в центре этой окружности показывает, сколько в угле угловых градусов. Прямой угол содержит 90°, острый угол — меньше 90°, тупой угол — больше 90 .


Реклама:



Читать далее:



Статьи по теме:


Главная → Справочник → Статьи → Блог → Форум