Кристаллографические символы

Категория:
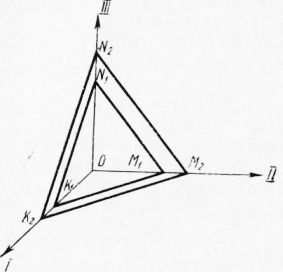
Обработка алмазов


Кристаллографические символы

Помимо вышеуказанных элементов симметрии для более точного представления о кристалле, необходимо выяснить взаимное расположение граней в пространстве. С этой целью применяют кристаллографические символы, определяющие положение любой грани данного кристалла относительно некоторых координатных осей и некоторой грани, принятой за исходную.

Понятие о символах вытекает из важнейшего закона кристаллографии — закона рациональности отношения параметров. Этот закон был открыт в конце XVIII в. французским ученым Гаюи на основании его теории внутреннего строения кристаллов. Согласно закону, на одном кристалле могут встречаться только такие фигуры, параметры граней которых относятся к параметрам граней простой формы, принятой за основную, как рациональные числа.
Грань, пересекающая все кристаллографические оси на самых коротких расстояниях от нулевой точки этих осей, называется единичной гранью, а отсекаемые ею на кристаллографических осях отрезки— единичными отрезками (параметрами).

Выбор кристаллографических осей должен удовлетворять основному условию: все грани одной и той же простой формы должны получать в данных осях одинаковые индексы.

Закон рациональности отношений параметров может быть сформулирован следующим образом: двойные отношения параметров, отсекаемых двумя любыми гранями кристалла на трех пересекающихся ребрах, равны отношениям целых чисел.

В кристаллографии обычно пользуются обратным отношением параметра грани, выбираемой за единичную, к параметру определяемой, т. е. делят величину отрезка, отсекаемого определяемой гранью. Получающиеся таким образом данные называются индексами граней и обозначаются символами h, k, I (величина h — характеризует индекс по оси I, k — по оси II, I — по оси III). Закон рациональности отношений параметров формулируется иначе: индексы граней кристаллов всегда выражаются простыми целыми числами.

В кристаллах кубической сингонии, к которой принадлежит алмаз, всегда присутствуют три взаимно перпендикулярные оси симметрии либо четвертого, либо второго порядка. Эти три оси принимаются за кристаллографические оси. В случае наличия кристаллографические оси проводятся по ним. Ряды пространственной решетки, соответствующие трем упомянутым осям, будучи связаны между собой тройной осью симметрии, обладают одинаковыми промежутками.

Рис. 1. Параметры граней

Параллелепипеды, слагающие любую кубическую решетку, имеют форму куба. На этом основании за единичную грань в кубическом кристалле следует принимать такую, которая по всем трем кристаллографическим осям отсекает равные отрезки.

Такому условию удовлетворяют грани тетраэдра или октаэдра. Поэтому их символ будет. При описании кристаллов обычно полную совокупность всех граней одной простой формы принято условно характеризовать символом одной из граней, обладающей наибольшим количеством положительных индексов. Например, вместо шести символов граней куба (100), (010), (001), (100), (ОТО), (001) употребляют лишь один (100).

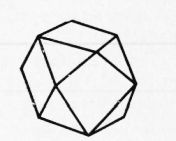
Рис. 2. Комбинация куба и октаэдра


Реклама:



Читать далее:



Статьи по теме:


Главная → Справочник → Статьи → Блог → Форум