|
|
Категория:
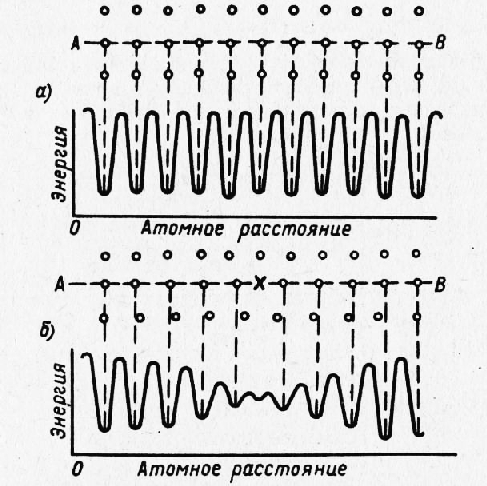
Металлы Рассмотрение процесса пластической деформации как одновременного смещения одного атомного слоя относительно другого на величину, кратную параметру решетки, является весьма упрощенным и требует известных уточнений. Если решетка кристаллита не подвергалась пластической деформации и соответствует равновесному состоянию металла, то атомы занимают в ней положения, которые характеризуются минимальным запасом внутренней энергии. Смещение атома из такого положения равновесия в любое промежуточное вызывает противодействие соседних атомов. Это противодействие является максимальным при смещении атома на половину параметра решетки и представляет собой своеобразный потенциальный энергетический барьер, который нужно преодолеть, чтобы переместить атом в новое положение равновесия. Атом, «поднятый» на вершину этого барьера, сам «падает» с него в новое положение равновесия, соответствующее минимальному запасу внутренней энергии. На рис. 57,а представлена модель равновесной пространственной решетки металла со схемой роста энергии при смещении атома из равновесного в промежуточное положение. На схеме видно, что равновесные атомы обладают минимумом энергии и находятся в своеобразной энергетической «яме». Для перемещения атома в соседний узел требуется как бы «извлечь» его из этой «ямы», т. е. преодолеть потенциальный барьер. Если представить себе пластический сдвиг упрощенно и допустить одновременное преодоление многочисленных потенциальных барьеров, то пришлось бы иметь дело с очень большими сдвигающими напряжениями, необходимыми для начала процесса пластической деформации. Однако известно, что эти начальные напряжения сдвига весьма невелики. Поэтому целесообразно допустить возможность не одновременного, а последовательного смещения атомов в плоскости сдвига, требующего преодоления гораздо меньших потенциальных барьеров, а следовательно, приложения извне меньших напряжений сдвига. Такое смещение можно представить при наличии несовершенств в кристаллической решетке, изменяющих энергетическое состояние кристаллической решетки (рис. 57,6). Несовершенства решетки приводят к местному снижению потенциальных барьеров и облегчают последовательное перемещение атомов.
Рис. 1. Энергетические условия сдвига в идеальной (а) и реальной (б) атомной решетке
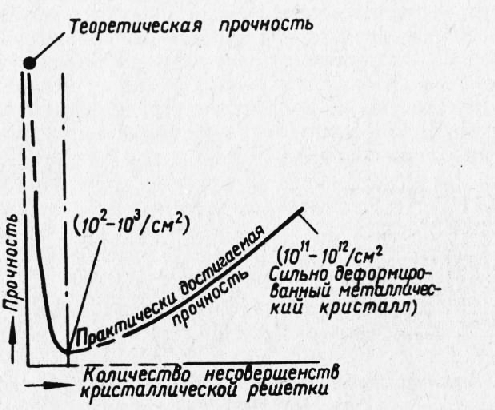
Прочность и пластичность кристаллических тел чрезвычайно сильно зависят от степени совершенства строения их пространственных решеток. Монокристаллы с абсолютно правильным строением кристаллической решетки должны обладать очень высокой так называемой теоретической прочностью. Обычные чистые монокристаллы не имеют такого идеального строения и, как правило, обладают низкой прочностью и высокой пластичностью. Хлористое серебро (точка плавления 445 °С) при 20 °С легко прокатывается в пластинку. Алюминий (точка плавления 660 °С) на холоду уже при очень малых напряжениях Деформируется пластически. Теллур (точка плавления 452 °С) при комнатной температуре пластически деформируется под влиянием собственного веса. Начальное сопротивление сдвигу чистых металлических монокристаллов составляет величину от сотых и десятых долей до немногих килограммов на квадратный миллиметр; следовательно, при столь малых напряжениях монокристаллы уже испытывают пластические деформации. В то же время по расчетам советского физика Я. И. Френкеля монокристаллы с идеальным атомным строением должны обладать критическим напряжением сдвига ос в сотни и нередко в тысячи раз большими. Зависимость прочности монокристалла от количества несовершенств в его пространственной решетке представлена на рис. 2. Из нее следует, что при отсутствии дефектов строения решетки монокристалл обладает высокой (теоретической) прочностью. При малом числе дефектов, приходящихся на единицу поперечного сечения монокристалла, прочность резко падает до минимума. Однако при увеличении числа дефектов, что может быть достигнуто преднамеренно путем применения ряда методов (см. далее), прочность может быть ощутимо увеличена; тем не менее она остается значительно более низкой по сравнению с теоретической.
Рис. 2. Зависимость прочности кристалла от количества несовершенств кристаллической решетки
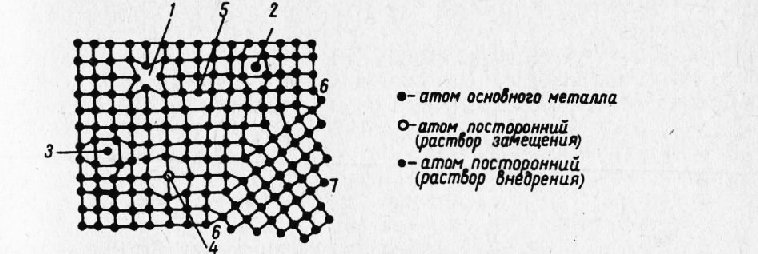
В соответствии с современными представлениями на рис. 3 приведена схема, систематизирующая несовершенства кристаллического строения на примере простой кубической решетки.
Рис. 3. Плоскостная схема простой кубической решетки с типичными несовершенствами строения
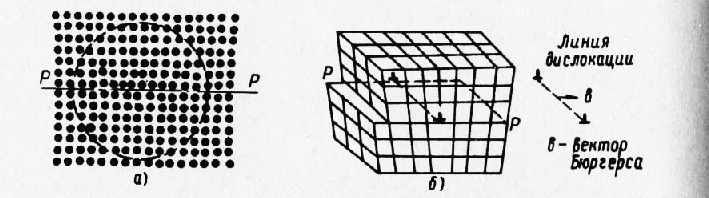
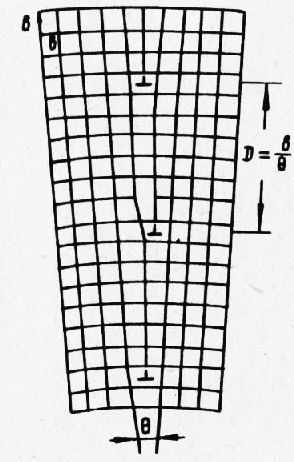
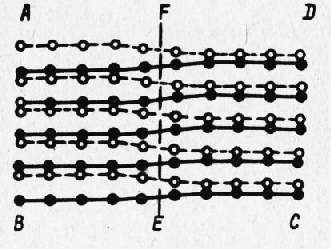
Рис. 4. Линейная (краевая) дислокация в простой кубической решетке:
а — плоскостная схема; б — пространственная схема
На схеме рис. 3 отчетливо заметно, что все виды несовершенств обязательно приводят к сосредоточенным или более или менее распространенным искажениям пространственной решетки в результате изменения межатомных расстояний в областях, соприкасающихся с местами нахождения дефектов. Область на рис. 3 характеризует зерно с идеальной решеткой. В настоящее время дислокации разных видов (краевые, винтовые, смешанные) рассматриваются как важнейшая особенность кристаллического строения. Преднамеренно создавая необходимое количество дислокаций, распределяя и закрепляя их в пространственной решетке, можно весьма существенно изменить показатели прочности и служебные свойства различных материалов. На этом основании целесообразно более подробно ознакомиться с элементами теории дислокаций. На рис. 4 представлена схема так называемой краевой или линейной дислокации Тэйлора. По этой схеме дислокация является местной неправильностью в расположении атомов, сосредоточенной около определенной плоскости РР, именуемой плоскостью дислокации. Типичным для названной дислокации является то обстоятельство, что горизонтальные ряды атомов, лежащие выше линии РР, содержат каждый на один атом больше, чем ряды, расположенные ниже этой линии. Это имеет место как в плоскости ри-сунка, так и в ряде параллельных ей атомных плоскостей, расположенных от нее по обе стороны. Неравенство числа атомов в верхних и нижних атомных слоях приводит к искажению кристаллической структуры. Искажение пространственной решетки носит местный характер и ограничено для каждой атомной плоскости примерно так, как показывает пунктирная окружность, центр которой является центром дислокации (начало координат). Если вглядеться в область, ограниченную пунктирной окружностью, то легко обнаружить, что вблизи центра дислокации атомы, лежащие выше линии РР, сильно сближены, а лежащие ниже этой линии раздвинуты по сравнению с атомами равновесной решетки. По мере удаления от центра искажение быстро уменьшается и на расстоянии радиуса практически исчезает. За пределами окружности решетка принимает нормальный вид. Если в плоскостях, параллельных рисунку, расстройство решетки ограничивается областью, очерченной пунктирной окружностью, то в направлении перпендикулярном искажение захватывает значительную часть кристалла или даже весь кристалл. Характерным является то обстоятельство, что в верхней части кристалла, лежащей над плоскостью дислокации, расположена атомная полуплоскость, являющаяся как бы лишней и отсутствующая в нижней части кристалла. Линия пересечения этой полуплоскости с плоскостью дислокации РР называется линией дислокации. На этом основании описываемое несовершенство получило название линейной или краевой дислокации. Пространственное представление об этом виде дислокации дает рис. 5,б. В идеализированном случае линия дислокации является прямой. Однако в действительности она чаще всего оказывается кривой. Под действием внешнего поля напряжений линия дислокации способна перемещаться в плоскости дислокации, причем направление и величина перемещения характеризуются вектором, или так называемым вектором Бюргерса. Наиболее типичным случаем является перемещение линии дислокации на один параметр решетки, когда вектор Бюргерса направлен перпендикулярно к линии дислокации. Такое перемещение дислокации, протекающее последовательно от атома к атому, очень быстро пробегает через весь кристалл и заканчивается пластической деформацией (сдвигом) на один параметр. Перемещение это протекает очень легко и требует приложения чрезвычайно незначительных напряжений, в сотни раз меньших по сравнению с расчетными. Для одновременного смещения на один параметр всех атомов в плоскости РР потребовалось бы, как было сказано ранее, огромное напряжение. Пробег дислокации весьма упрощенно, но очень наглядно можно сравнить с разглаживанием складки на расстеленном ковре. Складка под действием сравнительно небольшого усилия легко пробегает по ковру, а ковер в целом оказывается перемещенным по полу на некоторую величину. Само собой разумеется, что для одновременного смещения ковра на ту же величину потребуется гораздо большее усилие. Краевые дислокации подразделяются по знаку. Если лишняя атомная полуплоскость имеется сверху плоскости РР, то дислокация условно называется положительной и обозначается L, если снизу этой плоскости, — то отрицательной и обозначается Т. Легко видеть, что поворот на 180° превращает положительную дислокацию в отрицательную и наоборот (рис. 5).
Рис. 6. Положительная дислокация в металлическом кристалле.
Различать знак дислокаций полезно в связи с тем, что одноименные дислокации при движении через решетку склонны отталкиваться, а разноименные притягиваться друг к другу. Поскольку под влиянием напряжения краевая дислокация может перемещаться в плоскости дислокации, принято считать, что для положительной дислокации движение осуществляется слева направо (рис. 6,б), а для отрицательной—справа налево. Итак, пробег положительной или отрицательной дислокации завершается сдвигом одной части кристалла по другой на один параметр точно так же, как если бы смещение происходило по всей плоскости сдвига одновременно, а не последовательно, причем этот процесс протекает при воздействии очень небольших внешних сил. Теория дислокаций удовлетворительно объясняет возникновение сдвига при относительно небольших напряжениях при том условии, что на возможной плоскости сдвига зародилась и присутствует дислокация. Расчет показывает, что, например, в положительной дислокации, находящейся в поле сдвигающих напряжений, все атомы, за исключением центрального, находятся под действием сил разного знака, строго сбалансированных для каждой пары атомов, симметричной относительно центра дислокации. Поэтому каждая такая пара атомов, а следовательно, и дислокация в целом чрезвычайно легко передвинется в плоскости сдвига, включая и центральный атом, требующий для своего смещения очень небольшого напряжения. Важно подчеркнуть, что деформация совершенного кристалла, если в нем зародилась дислокация, протекает очень быстро. Интересно отметить, что краевая дислокация способна двигаться еще и в направлении, перпендикулярном плоскости сдвига, за счет взаимодействия с другим дефектом решетки в виде атомных дырок (вакансий). Это перемещение, однако, протекает весьма медленно.
Рис. 7. Модель кристаллической решетки с линейной (краевой) дислокацией
Понятие дислокации является довольно отвлеченным и представляет известные трудности при истолковании его физической сущности. Тем больший интерес представляют экспериментально построенные модели дислокаций, использование которых подтверждает ряд теоретических воззрений и позволяет установить закономерности, в свою очередь подтверждаемые опытом на реальных кристаллах. На рис. 7 изображено скопление многочисленных мыльных пузырьков одного размера, созданное по способу Брэгга с целью наглядно моделировать кристаллическую решетку и получить на ней структуры с дислокациями. При помощи этой модели доказано, например, что небольшое смещение пузырьков с их равновесного положения в правильной решетке приводит к образованию (рис. 7) устойчивой краевой Дислокации положительного знака. Кроме линейной, или краевой теория дислокаций описывает еще винтовые и частичные дислокации различных видов. Большой интерес представляет вопрос о плотности дислокаций в кристалле, т. е. о числе дислокационных линий, пересекающих единицу площади сечения кристалла. В наиболее совершенных практически получаемых кристаллах значения плотности дислокаций лежат в пределах 102—103 на см2; монокристаллы металлов и кристаллы в отливках после пластической деформации и отжига характеризуются плотностью дислокаций от 105 до 109 на см2, для сильно деформированных металлических кристаллов плотность дислокаций равна 10й—1012 на см2. При плотности 10” на см2 одна дислокация приходится на квадратную площадку со стороной, примерно равной 100 параметрам решетки (например, алюминия или меди).
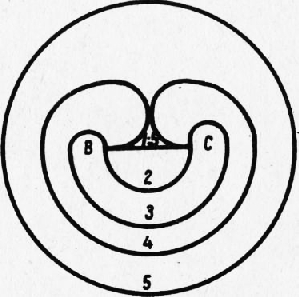
Рис. 8. Скопление дислокаций
Рис. 9. Объемная сетка дислокаций
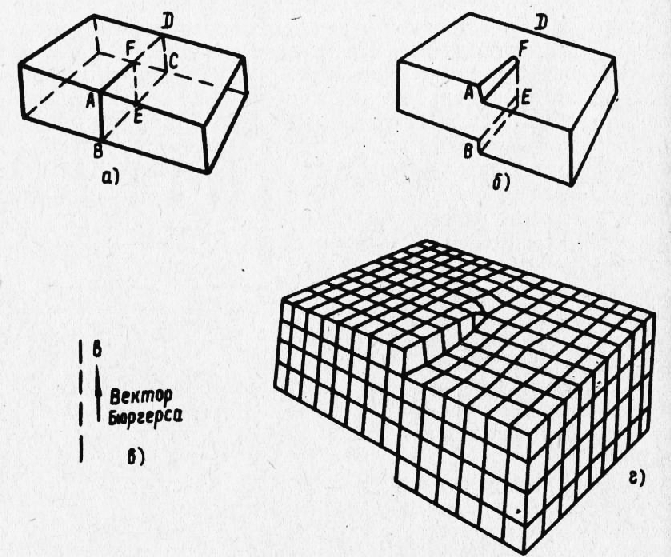
В отожженных монокристаллах и в кристаллах литого металла дислокации скапливаются главным образом в границах зерен, имеющих малый угол разориентировки (рис. 8), или образуют объемную сетку (рис. 9). Под влиянием касательных напряжений (напряжений сдвига) дислокации способны размножаться, т. е. увеличиваться в числе, возникая из определенных участков пространственной решетки. По современным представлениям на каждой активной плоскости скольжения в кристалле имеется источник дислокаций Франка—Рида. Таким источником является дислокация, у которой один или оба конца закреплены и не могут передвигаться в плоскости скольжения под действием приложенной нагрузки. При одном закрепленном конце (одноконечная дислокация) перемещаться сможет другой конец, а при двухконечной дислокации—средняя свободная часть. При этом единственный возможный способ движения дислокации это выгибание ее в дугу. Схема размножения линейных дислокаций по Франку и Риду представлена на рис. 10, где изображены этапы 1-5 образования дислокационных петель из начального отрезка линии дислокации ВС. Цикл из указанных этапов может повторяться многократно, поскольку при переходе от этапа 4 к этапу 5 и образовании отдельной дислокационной петли 5 внутри петли остается отрезок, на котором весь процесс способен повториться. Каждый полный цикл приводит к сдвигу на один параметр. Многократное повторение цикла позволяет протекать деформации сдвига по одной и той же плоскости на многие сотни параметров. Указанный механизм весьма просто и наглядно объясняет как макроскопические деформации сдвига, так и огромную плотность дислокаций в пластически деформированных кристаллах. Другим видом является дислокация винтовая, описанная Бюр-герсом. Схема кристалла с винтовой дислокацией представлена на рис. 66. В этом случае тело кристалла как бы надрезано полуплоскостью ABEF, причем надрез ограничивается линией FE (рис. 11,а); правая часть кристалла смещена по надрезу вниз так, что ее передняя грань сдвинулась по отношению к левой части кристалла на один параметр. Линией дислокации здесь окажется линия FE (рис. 11,6). Вектор Бюргерса, указывающий направление сдвига, в отличие от краевой дислокации будет не перпендикулярен, а параллелен линии дислокации (рис. 11,в).
Рис. 10. Схема размножения дислокаций по Франку и Риду. Последовательные этапы 1-5 образования дислокационных петель могут повторяться многократно
Рис. 11. Винтовая дислокация:
На рис. 11, г представлен выход винтовой дислокации в виде ступеньки на поверхность кристалла. Винтовая дислокация, вызывая смещение атомов, искажает пространственную решетку так, как изображено на рис. 67 для плоскости ABCD. Сплошными кружками и линиями представлены решетки правой части кристалла, претерпевшей смещение, а пунктирными кружками и линиями — решетка левой несмещенной части кристалла. Из рис. 66 и 67 видно, что искажение решетки наблюдается в основном непосредственно вблизи линии дислокации FE. Это искажение характеризуется тем, что все атомные плоскости, пронизанные линией дислокации, искажаясь, сливаются в одну атомную геликоидальную поверхность, напоминающую винтовую лестницу без ступенек.
Рис. 12. Атомная структура винтовой дислокации
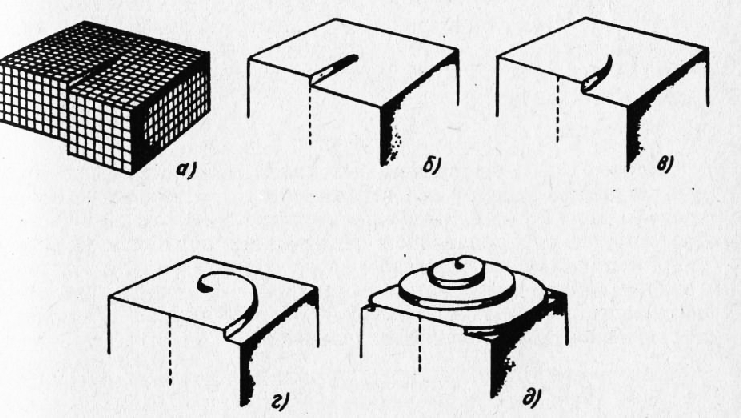
Рис. 13. Последовательные этапы спирального роста кристалла от ступеньки винтовой дислокации (а)
Винтовые дислокации облегчают рост кристаллов, так как ступенька, образовавшаяся на грани кристалла, является местом присоединения атомов при кристаллизации и обусловливает спиральный рост грани, как показано на рис. 13. Прикладное значение теории дислокаций состоит в ее использовании для упрочнения металлических материалов. При этом исходят из следующих основных положений. 1. Торможение дислокаций Поскольку малая прочность и высокая пластичность кристаллов связаны с пробегом дислокаций, целесообразно затормозить движение дислокаций. 2. Увеличение плотности дислокаций Известно, что прочность растет с количеством несовершенств и в первую очередь с количеством дислокаций в решетке. Поэтому целесообразно увеличивать плотность дислокаций в металлических материалах, одновременно принимая меры для торможения пробега дислокаций при обычных и повышенных температурах. 3. Устранение дислокаций Наивысшая прочность достигается при полном отсутствии дислокаций в кристалле. Получение совершенных кристаллов является большой проблемой. Она успешно решается пока для нитевидных кристаллов небольшой длины, так называемых кристаллических усов, по-видимому имеющих не более одной единственной дислокации и обладающих прочностью, приближающейся к теоретической. Из названного уравнения следует, что о растет с уменьшением L. Действительно, в начале процесса старения частиц второй фазы мало, расстояние L между ними велико, а прочность, характеризуемая напряжением о, мала. При завершении старения, когда число тончайших частиц второй фазы достигает максимума, расстояние L минимально, а прочность приобретает максимальное значение. Торможению дислокаций способствуют также границы зерен. В твердых растворах, не выделяющих частиц второй фазы, повышение прочности вызывается действием растворенных атомов, закрепляющих дислокации. Котрелл показал, что около дислокаций растворимость инородных атомов выше, чем в областях кристалла, не претерпевших искажения решетки. Поэтому вокруг каждой дислокации возникает как бы облако растворенных атомов (атмосфера Котрелла), мешающее передвижению атомов, что ведет к упрочнению кристалла. Известно, что пластическая деформация на холоду увеличивает прочность металлических материалов и уменьшает их пластичность. Это явление, часто именуемое наклепом, объясняется увеличением плотности дислокаций до весьма высоких значений. Перечисленные виды упрочнения за счет действия частиц второй фазы, атмосферы Котрелла и наклепа теряют эффективность с повышением температуры до такого уровня, когда становятся ощутимыми процессы диффузии. Поэтому сплавы для использования при высоких температурах должны разрабатываться с учетом необходимости уменьшить скорость диффузионных процессов и обеспечить более высокий температурный предел надежной службы таких сплавов. Теория дислокаций получила значительное развитие и приобрела большое прикладное значение. Реклама:Читать далее:Холодная пластическая деформация и рекристаллизация, понятие о горячей деформацииСтатьи по теме:Главная → Справочник → Статьи → Блог → Форум |
|
|
|
|
Контакты: Сергей Королёв © 2007-2009 Pereosnastka.ru - информационный сайт о металло- и деревообработке. |
© Все права защищены.
Копирование материалов невозможно. |
|