Pereosnastka.ru

Преобразования

Преобразования

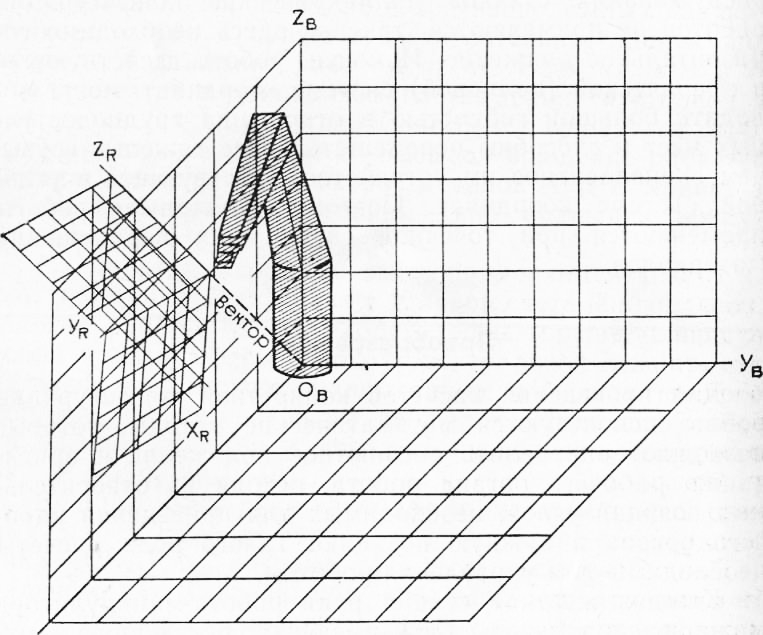
Для проведения расчетов конкретной конфигурации робота используются математические методы, которые позволяют определить абсолютное положение и ориентацию рабочего органа робота, исходя из относительных позиций узлов, необходимых для приведения рабочего органа в нужную позицию. Такого рода расчеты необходимы для управления роботом.

Каждая жесткая секция руки робота-манипулятора может рассматриваться как имеющая собственную замкнутую систему координат. В этом случае необходимо определить положение и ориентацию системы координат относительно базовой системы, чтобы фактически вычислить позицию секции руки робота. На рис. 1 представлено абсолютное положение рассматриваемой секции робота (например, рабочего органа) по отношению к выбранной базовой системе (система координат — прямоугольная). Базовая система, например, могла бы быть так выбрана, что начало ее координат приходилось на центр базы робота с горизонтальной плоскостью X—Y с осью Y. Эквивалентную систему координат относительно заданной секции руки робота можно рассматривать как «плавающую» в пределах базовой системы.

Для описания начального положения второй системы координат (см. рис. 1) можно лишь определить направление вектора из начала координат Ов базовой системы к началу второй системы. Однако это не дает информации об ориентации второй системы. Математически ориентацию можно определить, используя матрицу размерностью 3X3. Три величины в столбце представляют точки X, Y и Z ориентации отдельной оси второй системы так, как если бы она была прямой линией в базовой системе. Определяя таким образом ориентацию для каждой из трех осей второй системы (беря три столбца матрицы), можно определить ориентацию второй системы.

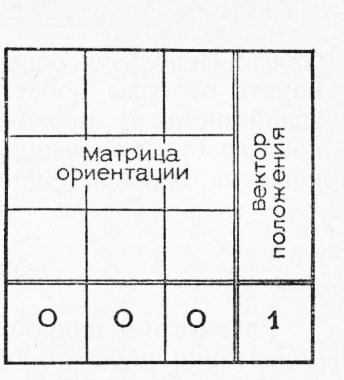
Для того чтобы определить координаты любой точки рассматриваемой секции робота, необходимо произвести некоторые действия под вектором. На практике это осуществляется с помощью однородного преобразования с использованием легко составляемой матрицы размерностью 4X4 (рис. 2) путем присваивания положению вектора матрицы ориентации цифр 0001. В этом виде преобразование можно сделать умножением координат точки во второй системе (в форме X, У, Z, 1, где 1 — масштабный фактор) на однородную матрицу преобразования.

На практике не всегда возможно определить набор вторичных систем координат в терминах базовой системы. Во-первых, роботы не состоят из серий независимых секций, «плавающих» в базовой системе,— секции связаны друг с другом последовательно. Во-вторых, положения обслуживаемых объектов (таких, как детали в палете), которые не связаны с роботом, могут оставаться неподвижными относительно друг друга, но не относительно базовой системы.

Чтобы учесть эти факторы, можно применить однородные преобразования для описания положений и ори-ентаций относительно друг друга двух систем координат, отличающихся от базовой системы. В этом случае координаты каждой детали на палете, например, задавались относительно палеты. Применяя относительные преобразования, которые описывают зависимость между объектами и палетой, можно было бы сравнительно легко определить абсолютные координаты объектов в точке покоя.

Таким образом, связывая вместе ряд вычислений относительных преобразований, можно выработать цепь Различных систем, в которых известны только относительные положения и ориентации соседних систем. Наиболее важным звеном цепи обыуло является рука робота. Используя относительные преобразования, можно начать от базы робота (закрепленной относительно базовой системы), проходя через каждый узел по очереди, пока не будет определено абсолютное положение (в отношении базовой системы) самого рабочего органа.

Читать далее:

• Когда-то, никогда
• 2000—2050
• 1990—2000
• 1984—1990
• Проблемы прогнозирования