|
|
Категория:
Совершенствование производства Определение общих для групп деталей свойств и выделение единых признаков этих свойств, пригодных для решения различных производственно-технических задач — унификации деталей и технологических процессов их изготовления, механизации и автоматизации технологической подготовки производства, механизации учета и различных расчетов на всех этапах подготовки ведения производственного процесса — является особенно важным в условиях многономенклатурного мелкосерийного машиностроительного производства с часто меняющейся структурой про-зводственной программы. Решение этой задачи позволяет наиболее ффективно и целесообразно осуществлять максимально комплекс-е совершенствование и автоматизацию всей системы управления производством. Для правильного понимания механизма формирования При знаков, необходимых и достаточных для решения поставленных нами задач и для решения вопроса о значности кода этих призна. ков, уточняющих высшие классификационные группировки ORn (в том числе и размерную характеристику детали), необходимо остановиться на одном из вопросов теории. Это вопрос о регулирующей функции сигнала информации в управляющих системах и о связи системы классификации и кодирования со стандартизацией. В различных системах классификации при определении состава признаков, учитываемых в цифровом коде деталей, мы сталкиваемся со следующей альтернативой. Для того чтобы было возможным с помощью классификационного шифра детали решать самые различные по характеру технические, организационные и экономические задачи, необходимо в соответствии с принятой системой классификации закодировать конструкцию (геометрическую форму) детали, ее качественные характеристики (материал, термическая обработка, шероховатость поверхности, вид покрытия), а также значение и положение каждого ее элемента. Однако в этом случае деталь приобретает слишком большой цифровой код, использование которого для практических целей чрезвычайно затрудняется. Путем исключения из кода детали ряда признаков (или их укрупнения) можно значительно уменьшать ее цифровой код, но тем самым уменьшать и полноту представления о детали, а значит, сужать и круг решаемых с помощью ее цифрового кода задач. Однако ни то, ни другое решение не может нас удовлетворить. Здесь встает вопрос: существует ли методический прием, с помощью которого становится возможным получить полное представление о конструктивных, технологических и эксплуатационных особенностях детали, размерах и положении каждого ее конструктивного элемента (т. е. ее полной размерной характеристике) при достаточно коротком цифровом коде? Отыскание указанного методического приема позволило бы значительно расширить класс решаемых с помощью классификационной системы задач. Особенно важным является то, что с помощью единой классификационной системы удалось бы решать задачи заимствования, унификации, механизации и автоматизации разработки технологических процессов, трудовых и материальных нормативов, механизации и автоматизации различных расчетов, связанных с планированием, учетом и регулированием производства. Такая система, значительно упростив процесс классификации и кодирования, позволила бы намного снизить трудоемкость всех работ, предшествующих машинной обработке информации, и более рационально использовать материальные носители информации, сделав более содержательной и комплексной применяемую в расчетах единицу информации.
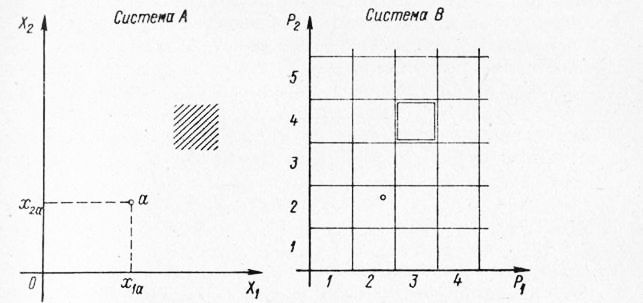
Рис. 45. Гомоморфизм пространств состояний систем Гомоморфизм является наиболее общей формой отношений множества — образа к множеству — праобразу. Рассмотрим пример. Известно, что состояние системы определяют ее координаты. Например, как видно из рис. 45, задавая координаты точки в системе А, мы однозначно задаем квадрат, определяющий состояние системы В (квадрат 2—2). Однако задание квадрата системы В не определяет однозначно положение какой-либо точки в системе А, так как заданному квадрату соответствуют все точки системы А, лежащие в заштрихованной области ее пространства состояний. В рассмотренных нами случаях состояние системы А однозначно соответствует состоянию системы В, но оба случая перехода от Л к В приводят к неоднозначности обратного соответствия. Таким образом, система В, полученная из исходной системы А за счет ее упрощения (либо за счет уменьшения числа рассматриваемых координат, либо за счет более грубой оценки их значений), и является гомоморфной или упрощенной моделью системы А. тношения между оригиналом и его гомоморфной моделью являются неравноправными (система А не может рассматриваться как гомоморфная модель системы В). Из сказанного следует, что замена пространства состояний включающего множество значений его координат, пространством, состоящим из нескольких (или одного) указанных состояний’ означает переход от оригинала к его гомоморфной модели. В том случае, когда однозначное соответствие обоих множеств и отношений между ними становится взаимным, гомоморфизм переходит в изоморфизм. Изоморфными называют системы, характеризующиеся одинаковыми наборами входных и выходных величин и одинаково реагирующие на внешние воздействия. Другими словами, только в том случае два множества являются изоморфными, если их элементы попарно взаимно однозначно соответствуют друг другу и функции, выражающие отношения элементов в одном множестве, взаимно однозначно сопоставляются с функциями, выражающими отношения между соответствующими элементами в другом множестве. Вот именно эта форма взаимной упорядоченности двух множеств состояний — носителя информации и множества-источника — делает сигнал кодом информации. Из сказанного следует, что поскольку сигнал изоморфен источнику (упорядоченность источника изоморфно воспроизведена в сигнале), объективные характеристики источника, распределение вероятностей его состояний и его физическая энтропия переносятся на сигнал. Поэтому множество состояний носителя, формирующее сигнал, несет информацию о всех элементах и отношениях множества-источника. Фигура, представленная на рис. 46, является кодом всех деталей данной конструкции, т. е. имеющих в своем составе аналогичный набор элементов, расположенных в той же последовательности. Данный сигнал-код может быть выражен математически в виде формул или в виде цифрового кода, т. е. выражен в другом алфавите, но и в этом случае он будет кодом всех деталей, конструкция которых может быть представлена рис. 46. Именно в таком, не нарушающем отношений изоморфизма изменении характеристик и их отношений в множестве, образующем сигнал-код; и состоит сущность перекодирования сигнала. Из приведенного на рис. 46 сигнала-кода можно видеть (он несет эту информацию), что одни элементы больше (или меньше) других, известен порядок следования (взаимоположения) элементов, но размеры элементов и их координаты не заданы. Именно поэтому приведенный нами образ изоморфен множеству множеств праобразов-деталей.
Рис. 46. Изображение — сигнал, изоморфно воспроизводящий все детали данной конструкции Для того чтобы стала возможной реализация регулирующей функции сигнала, необходимо, чтобы информация, осуществляющая регулирование, соответствовала данному источнику в его конкретной специфике, которая отличает этот источник от других изоморфных ему объектов. Л. М. Веккер пишет по этому поводу: «Чтобы устранить неоднозначность отношений кода к его источникам, т. е. чтобы от кода вернуться к тому «индивидуальному» представителю множества всех изоморфных сигналу-коду множеств, который составляет именно данный источник информации, необходимо декодировать информацию. Необходимость декодирования сигнала, которое приводит сигнал в соответствие с конкретными структурными характеристиками данного источника, вытекает, таким образом, из самого существа изоморфных отношений кода к источнику, из тех оставляемых условиями изоморфизма избыточных степеней свободы сигнала, без преодоления которых адекватная регулирующая функция сигнала не может быть реализована» [8]. Именно в силу этого обстоятельства для того, чтобы однозначно соотнести код с объектом, конкретно в нем закодированном, необходимо однозначно жестко фиксировать функции, преобразующие множество-сигнал в множество-источник. Возвращаясь к нашему случаю (рис. 46), необходимо отметить следующее. Представим себе, что все детали, код которых изоморфно воспроизведен рис. 46, проектировались без заранее сформулированных числовых зависимостей между элементами как внутри одной детали, так и при переходе от одного типоразмера к другому, скажем, при возрастании определяющего элемента d. В этом случае для того, чтобы механизировать, например, отбор (счет) типоразмеров деталей с одинаковыми значениями конструктивных элементов, одной маркой материала, одним видом термической обработки и гальванического покрытия (без дополнительного анализа чертежей деталей «вручную»), необходимо осуществить кодирование не только конструкции, но и всех параметров детали, марки материала, вида термической и гальванической обработки, а также размеры и координаты каждого конструктивного элемента. Другими словами, для целей кодирования и однозначного декодирования информации необходимо, чтобы элементы и их отношения в множестве-образе не только однозначно соответствовали бы элементам и их отношениям в множестве праобразе, но и воспроизводили бы и сохраняли их конкретный характер. Именно это обстоятельство вынудило разработчиков системы яссификации, названной системой кодирования признаков ГлИТМО) и изложенной нами выше, отказаться от кодирования значения и положения каждого элемента детали и перейти к гомоморфной (упрощенной) модели, укрупнив кодируемые признаки. Теперь мы вплотную подошли к вопросу, который был задан нами в самом начале: можно ли, значительно упростив процесс кодирования за счет соответствующего «сжатия» информации (но без потери ее ценности), сделать код наиболее удобным для целей не только машинной обработки информации, но и для «ручного» поиска при унификации и заимствовании. При переходе от эмпирических законов к теоретическим происходит сжатие, сокращение информации за счет устранения избыточности. Устранение избыточности свидетельствует о том, что теория устанавливает взаимосвязь, корреляцию между эмпирическими законами. Чем больше теория устраняет избыточность из информационного содержания эмпирических законов, тем более информационноемкой она является [7]. Однако последнее в равной мере (в информационном аспекте) закономерно при отношении эмпирических законов к фактам. Д. П. Горский также высказывает мысль о том, что критерием, позволяющим отличить закон от простой регистрации установленных опытным путем фактов, является сокращение, сжатие информации. Он указывает, что если данную совокупность описываемых фактов, т. е. некоторую информацию не удается сократить, представив ее в форме, содержащей существенно меньшее число параметров, то мы имеем дело со случайной (во всяком случае, не закономерной) совокупностью событий. Если же такое «сокращение» удается осуществить и оно оказывается полезным в своих применениях, то это означает, что в этих событиях, их связях и соотношениях содержится нечто закономерное. Если рассматривать деталь только с позиций взаимозаменяемости, то среди всех ее элементов можно выделить основные (определяющие ее взаимозаменяемость) и второстепенные элементы. Исключение при классификации и кодировании второстепенных элементов позволяет значительно «сжимать» информацию, сокращая очень существенно цифровой код детали. Отношения же изоморфизма между деталью и ее кодом при этом нарушены не будут. Однако кодирование значений только существенных координат ноП°ВНЫХ элементов) возвращает нас к упрощенной (гомоморф-) модели, благодаря чему теряется значительная часть регулирующей функции сигнала информации, т. е. значительно с жается круг решаемых с помощью цифрового кода детали зада Для того чтобы этого не случилось, необходимо несуществе ные координаты системы (второстепенные элементы деталей не исключать вовсе из рассмотрения; они исключаются из рас смотрения только при кодировании деталей, а их зависимост от основных (определяющих) элементов должна быть зафиксиро вана соответствующими таблицами. Этот прием позволяет без потерь сохранить регулирующу функцию сигнала информации при значительном сокращени кода детали, т. е. ответить тем самым на вопрос, поставленный в начале этого параграфа. Естественно, конечно, что исключени из классификационной системы второстепенных элементов дета лей и фиксация их зависимостей от основных элементов не может осуществляться произвольно. Эти действия должны базироваться на исследовании и точной формулировке закономерностей во взаи мосвязях между основными и второстепенными элементами дета лей; Однако сама по себе точная формулировка этих зависимо стей не может увеличить регулирующую функцию сигнала информации — кода детали. Для того чтобы выявленные закономерные зависимости элементов деталей стали полезными в применении (могли «работать»), необходимо, чтобы они стали обязательными при проектировании, т. е. приобрели силу закона. Такое закономерное табличное задание зависимостей несущественных элементов от основных может быть осуществлено ‘только через стандарты, являющиеся обязательными на всех этапах проектирования и производства. В этом случае при машинной обработке информации возврат от кода основных характеристик к несущественным элементам деталей осуществляется за счет того, что функции зависимости несущественных элементов от основных вносятся в память ЭВМ и используются для целей распознавания и выполнения других работ с помощью вычислительной техники. Реклама:Читать далее:Повышение информационной емкости классификационных признаков и их кодаСтатьи по теме:
Главная → Справочник → Статьи → Блог → Форум |
|
|
|
|
Контакты: Сергей Королёв © 2007-2009 Pereosnastka.ru - информационный сайт о металло- и деревообработке. |
© Все права защищены.
Копирование материалов невозможно. |
|