Построение разверток

Категория:
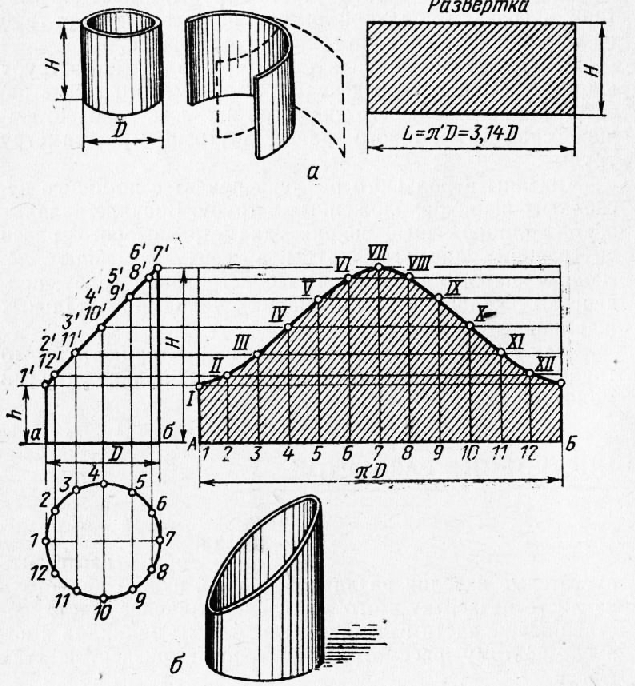
Медницко-жестяницкие работы


Построение разверток

Чтобы изготовить пустотелые изделия различной формы, нужно разметить на листе развертку этого изделия. Наиболее часто составляющие части изделия имеют формы цилиндра и конуса, поэтому рассмотрим построение разверток этих фигур.

Развертка прямого цилиндра представляет собой прямоугольник (рис. 1, а), ширина которого равна высоте цилиндра Н, а длина — длине окружности цилиндра. Для определения этой длины диаметр цилиндра D умножают на число 3,14, обозначаемое в формулах греческой буквой п.

Длина окружности цилиндра определится по формуле L = nD = 3.14D.

Например, если цилиндр имеет диаметр 100 мм, то длина развертки L = 3,14 • 100 = 314 мм. При этом расчете

he учитывают длину материала, идущего на соединительный шов. Полная длина развертки равна длине окружности плюс припуск на шов.

Рис. 1. Построение развертки цилиндра; а — прямого: о — усеченного

Развертка усеченного цилиндра представлена на рисунке 5 б. В натуральную величину вычерчены две проекции усеченного цилиндра: вид сбоку и вид сверху (план). Окружность круга (основания цилиндра) делят на несколько равных частей, проще всего на 12; в результате получают точки 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12. Эти точки соединяют линиями, перпендикулярными диаметру 1—7,

с наклонной линией верхней проекции 1‘—7’. При пересечении получают точки Г; 2’, 12’; 3’, 11’; 4’, 10’; 5’, 9’; 6’, 8’ и 7’. Вправо от верхней проекции проводят линию АБ, которая является продолжением линии аб (основания верхней проекции) и по длине равняется длине окружности основания цилиндра (L = 3,14D). Линию АБ делят на 12 равных частей. Из каждой точки на линии АБ восстанавливают перпендикуляры, а из каждой точки на наклонной Г—V проводят линии, параллельные прямой АБ, до пересечения с этими перпендикулярами. Пересечение линии, проведенной из точки 1’, с перпендикуляром, восстановленным из точки 1 на линии АБ, даст точку I развертки; пересечение линии, проведенной из точки 2’, с перпендикуляром, восстановленным из точки 2, даст точку II развертки и т. д. Соединив все полученные точки плавной кривой, получают развертку усеченного цилиндра в натуральную величину. Если изделие соединяется фальцевыми швами, к развертке прибавляют припуск на швы.

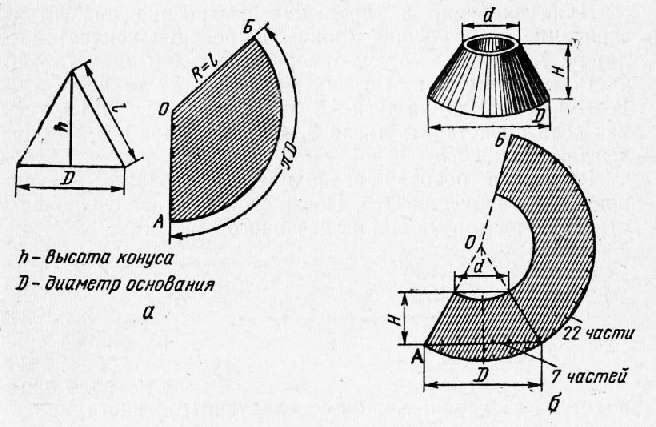
Рис. 2. Построение развертки конуса; а — прямого; б — усеченного

Развертка конуса приведена на рисунке 2а. Для ее построения вычерчивают в натуральную величину боковую проекцию конуса, которая представляет собой треугольник. Высота треугольника равна высоте конуса (h), а основание — диаметру окружности, лежащей в основании конуса (D). На боковой проекции конуса измеряют циркулем сторону треугольника, обозначенную на рисунке буквой, и, не изменяя развода циркуля, проводят рядом с проекцией часть окружности радиусом, равным. От точки А, лежащей на дуге этой окружности, откладывают расстояние, равное L = 3,14D. Для этого берут тонкую проволоку длиной L = 3,14D и от точки А откладывают ее по дуге. Там, где проволока кончится, отмечают точку Б и соединяют точки А и Б с центром О. Полученная фигура АОБ — развертка боковой поверхности конуса. При соединении конуса фальцевым швом прибавляют припуск на шов.

Для ускорения и упрощения построения развертки основание треугольника (боковой проекции конуса) делят на 7 частей, а затем, отмерив циркулем одну такую часть, откладывают от точки А по дуге 22 такие части. В этом случае длина дуги АБ будет равняться 3.14D, так как если представить число 3,14 простой дробью, то оно выглядит как 22/7.

Развертка боковой поверхности усеченного конуса показана на рисунке 2. Построение ее аналогично построению развертки для неусеченного конуса.


Реклама:



Читать далее:



Статьи по теме:


Главная → Справочник → Статьи → Блог → Форум