|
|
Категория:
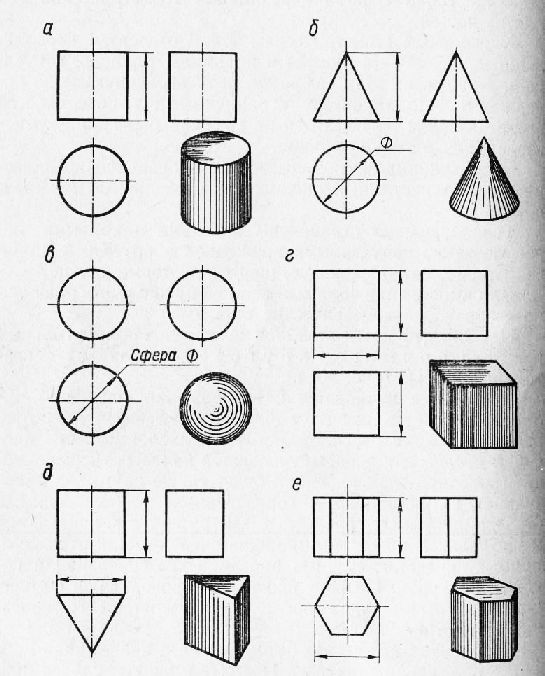
Технические чертежи Форма деталей, встречающихся в технике, представляет собой сочетание различных геометрических тел или их частей. К основным геометрическим телам относятся параллелепипед, различные призмы и пирамиды, цилиндр, конус и шар. Каждое из этих тел имеет свои ограничивающие поверхности. По характеру ограничивающих поверхностей геометрические тела делятся на две основные группы: многогранники и тела вращения. Многогранниками называются тела, ограниченные плоскими поверхностями: параллелепипед, различные призмы и пирамиды. Тела вращения ограничены плоскими и кривыми поверхностями, полученными вращением образующей линии вокруг оси: цилиндр, конус, шар и некоторые другие. Для выполнения чертежей деталей нужно уметь правильно изображать геометрические тела. Наиболее простым является построение прямоугольных проекций прямого кругового цилиндра с вертикальной осью. Построение начинается с изображения основания цилиндра, представляющего собой плоскую фигуру — круг. Поскольку круг расположен параллельно плоскости проекций и, следовательно, изображается на ней без искажений, его горизонтальная проекция будет также кругом, а фронтальная и профильная — горизонтально расположенными отрезками прямых, равными диаметру круга. Фронтальная и профильная проекции цилиндра очерчиваются отрезками прямых, представляющими проекции его оснований и боковых контуров. На всех проекциях проводят оси симметрии. Размеры цилиндра определяются диаметром его основания и высотой. Из рисунка видно, что фронтальная и профильная проекции цилиндра одинаковы. Поэтому в данном случае профильная проекция лишняя. Однако чертежи всех геометрических тел выполнены в трех проекциях, чтобы показать, какие проекции они имеют.
Рис. 1. Проецирование основных геометрических тел.
Построение изображений конуса вращения (рис. 1,б) во многом сходно с построением изображений цилиндра. Горизонтальная проекция конуса представляет собой круг, на котором пересечением центровых линий показана проекция вершины конуса. Диаметр круга равен диаметру основания конуса. Два других изображения конуса представляют собой равнобедренные треугольники, высота которых равна высоте конуса. На этих проекциях проводят оси симметрии. Для конуса указывают диаметр его основания и высоту. На рис. 1, в представлены чертеж и наглядное изображение шара. Все-проекции шара — круги диаметром, равным диаметру шара. На каждом изображении проводятся центровые линии. Так же, как и шар, куб имеет три одинаковые проекции (рис. 1, г). К у б —это тело, все грани которого — квадраты, изображаемые на плоскостях проекций в натуральную величину. Размеры куба определяют три измерения — длина, ширина и высота. Построение изображения правильной треугольной призмы (рис. 1, д) следует начинать с основания, т. е. равностороннего ^треугольника, который располагают параллельно горизонтальной плоскости проекций. Поэтому горизонтальная проекция треугольной призмы представляет собой равносторонний треугольник. На фронтальной плоскости проекций задняя грань призмы изображается в натуральную величину, а две передние грани — с искажением. Ширина прямоугольника, представляющего собой профильную проекцию, равна высоте треугольника основания призмы. На горизонтальной и фронтальной ^проекциях проводят осевые линии, на профильной проекции ось симметрии отсутствует. Построение прямоугольных проекций правильной шестиугольной призмы (рис. 1, е) также начинают с горизонтальной проекции, которая представляет собой правильный шестиугольник. На фронтальной проекции средняя грань изображается в натуральную величину, а ширина боковых граней искажена. На профильной проекции обе грани также изображаются искаженными по размерам. Размеры правильной шестиугольной призмы определяются ее высотой и шириной, равной удвоенной длине стороны основания. На рис. 1, ж приведены три проекции и наглядное изображение правильной четырехугольной пирамиды. Основание ее, параллельное горизонтальной плоскости проекций, как и в предыдущих случаях, проецируется в натуральную величину, т. е. представляет собой квадрат. Боковые ребра, идущие из вершин основания к вершине пирамиды, изображаются на нем диагоналями. Фронтальная и профильная проекции представляют собой равнобедренные треугольники, высота которых равна высоте пирамиды. На этих проекциях проводят оси симметрии, а на горизонтальной проекции необходимо провести две оси симметрии. Для правильной четырехугольной пирамиды наносят длины двух сторон основания и высоты. Аналогично построению изображений четырехугольной пирамиды строятся три проекции правильной шестиугольной пирамиды. Горизонтальной проекцией ее является правильный шестиугольник с диагоналями, изображающими боковые ребра. На фронтальной проекции показывают три грани, а на профильной — две. На фронтальной и горизонтальной проекциях ; проводят оси симметрии. Размеры правильной шестиугольной пирамиды определяются ее высотой и шириной, равной длине двух сторон основания. Реклама:Читать далее:Построение проекций вырезов на геометрических телахСтатьи по теме:Главная → Справочник → Статьи → Блог → Форум |
|
|
|
|
Контакты: Сергей Королёв © 2007-2009 Pereosnastka.ru - информационный сайт о металло- и деревообработке. |
© Все права защищены.
Копирование материалов невозможно. |
|