Простейшие геометрические построения

Категория:
Технические чертежи


Простейшие геометрические построения

Построением называется графический способ решения геометрических задач на плоскости при помощи чертежных инструментов.

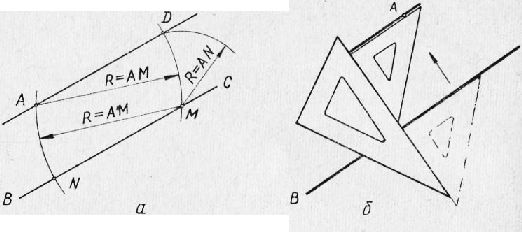
Рис. 1. Построение параллельных прямых: а — при помощи циркуля и треугольника; б — при помощи двух треугольников.

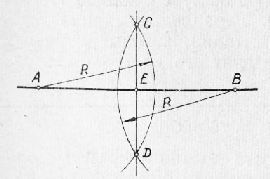
Построение параллельных прямых.

Через точку А, лежащую вне прямой ВС, провести прямую, параллельную ВС.
а) При помощи циркуля и треугольника (рис. 1, а). Приняв за центр произвольно расположенную на прямой ВС точку М, проводим при помощи циркуля дугу радиусом, равным AM, которая пересечет прямую ВС в точке N. Из точки А тем же радиусом, равным AM, проводим вторую дугу. Из точки М радиусом, равным AN, на этой дуге делаем засечку, получаем точку D. Через точки А и D при помощи треугольника проводим прямую, которая будет параллельна прямой ВС.
б) При помощи двух треугольников (рис. 1, б). Прикладываем катетодного треугольника к данной прямой ВС. К другому катету прикладываем второй треугольник и передвигаем первый треугольник по стороне второго в направлении, указанном стрелкой, до точки А. Через точку А вдоль катета треугольника проводим прямую, которая будет параллельна данной прямой ВС.

Деление отрезка прямой на равные части и построение перпендикуляров

1. Разделить прямую АВ на две равные части и построить перпендикуляр в середине отрезка.

а) При помощи циркуля и треугольника (рис. 2). Из концов отрезка АВ, как из центров, проводим две дуги радиусом R, размером несколько большим половины отрезка. Через точки пересечения дуг С и D проводим прямую, которая в точке Е разделит данный отрезок АВ на две равные части и в то же время будет перпендикуляром к отрезку АВ, проведенному через его середину.
б) При помощи двух треугольников (рис. 3). На отрезке прямой АВ дана точка С. Требуется построить отрезок прямой, перпендикулярный к отрезку АВ. Для построения подводим к отрезку АВ возможно точнее треугольник одним из его катетов. Оставляем этот треугольник неподвижным, подводим к его гипотенузе другой треугольник, лучше всего гипотенузой. Затем оставляем неподвижным второй треугольник, двигая первый по ребру второго, пока его второй катет не приблизится к точке С. Через заданную точку проводим прямую, которая и будет перпендикулярна к данной прямой АВ.

Рис. 2. Деление отрезка на две части и построение перпендикуляра к нему.

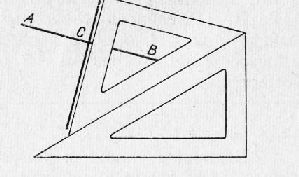
Рис. 3. Построение перпендикуляра к прямой в заданной точке.

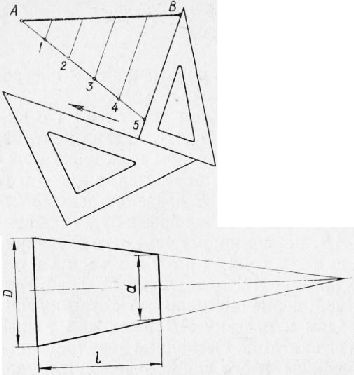
Рис. 4. Деление отрезка на пять равных частей.

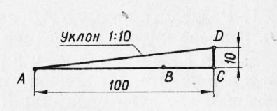
Рис. 5. Построение уклона к прямой.

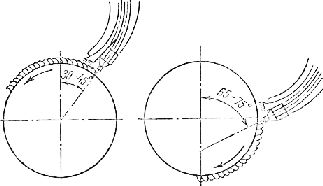
Рис. 6. Определение конусности.

2. Отрезок АВ разделить на любое число равных частей.

Допустим, что отрезок АВ необходимо разделить на пять равных частей (рис. 20). Из любого конца отрезка проводим луч под произвольным углом. Вдоль луча при помощи циркуля откладываем пять равных отрезков произвольной длины. Соединяем полученную точку 5 на луче с концом отрезка В. Передвигая треугольник параллельно линии 5В, через точки 4, 3, 2, 1 проводим линии, которые в точках пересечения с отрезком АВ разделят его на пять равных частей.

Построение уклонов и конусности

Величины уклона и конусности можно выразить дробью, процентами или углом в градусах. Уклоном прямой AD по отношению к прямой АВ называется отношение катетов прямоугольного треугольника ACD, т. е.

Рассмотрим построение линии с уклоном 1 : 10. Откладываем на прямой АВ, по отношению к которой строится уклон, десять (единиц) отрезков, равных 10 мм каждый; получим точку С. Из этой точки восстановим перпендикуляр к прямой АВ, на котором отложим отрезок, равный 10 мм (одной единице); получим точку D. Соединив точки А и D, строим линию уклона 1 : 10.

Построение других уклонов производится аналогично. Для определения величины уклона прямой достаточно измерить катеты и узнать их отношение.

Конусностью называется отношение разности диаметров “двух поперечных сечений конуса к расстоянию между ними (рис. 22), т. е. K = D~d, где D — диаметр большего основания конуса; d — диаметр меньшего основания конуса; I — длина усеченного конуса.

Следовательно, конусность равна 1 : 10, или 10%.

Построение углов
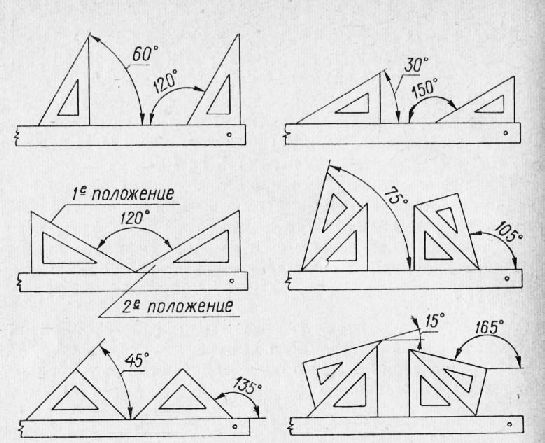
а) При помощи линейки и двух тре-угольниковс углами 30, 60, 90° и 45, 45, 90° производится легко и просто. На рис. 23 приведено построение углов от 15 до 165°.
б) При помощи циркуля и линейки. 1. Разделить прямой угол на два равных угла по 45° (). Для деления прямого угла пополам из вершины О угла АОВ, как из центра, проводим дугу произвольным радиусом R до пересечения ее со сторонами угла в точках а и b. Из точек а и b произвольным радиусом Ra, большим, однако, половины длины дуги ab, проводим дуги до пересечения их в точке К (в данном случае радиус Ra можно взять равным радиусу R). Точку К соединяем с точкой О. Прямая КО делит угол АОВ пополам, следовательно, углы АОК и КОВ равны каждый 45°. Прямая КО, делящая угол пополам, является биссектрисой угла.

Рис. 7. Построение углов при помощи линейки и двух треугольников.

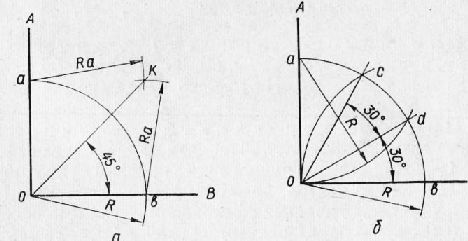
Рис. 8. Деление прямого угла: а — на две равные части; б — на три равные части.

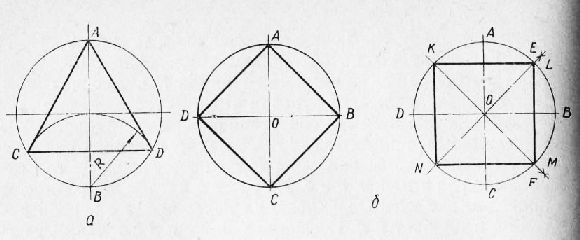
2. Разделить прямой угол натри равные части. Из вершины О прямого угла АОВ, как из центра, проводим дугу произвольным радиусом R до пересечения ее со сторонами угла в точках а и Ь. Из точек b и а тем же радиусом проводим две дуги Ос и Od до их пересечения с первой дугой ab в точках с и d. Соединив точки с и d с точкой О, получим три угла, каждый из которых равен 30°.

Деление окружности на равные части и вписывание в нее правильных многоугольников

1. Разделить окружность на три части и вписать в нее правильный треугольник.

Из конца какого-либо диаметра, например из точки В, как из центра, проводим дугу радиусом R, равным радиусу окружности. Пересечение этой дуги с окружностью даст точки С и D. Соединив их с точкой А и между собой, получим правильный треугольник A CD, вершины которого разделят окружность на три равные части.

2. Разделить окружность на четыре и восемь равных частей и вписать в нее квадрат и правильный восьмиугольник.

Двумя взаимно перпендикулярными диаметрами окружность уже разделена на четыре равные части. Соединив концы диаметров ABCD прямыми, получим вписанный в окружность квадрат ABCD. Если в окружность необходимо вписать квадрат со сторонами, параллельными полю чертежа, необходимо разделить дуги АВ и ВС на две равные части.

Деление дуг производится точно так же, как и деление отрезка на две равные части. Из точек А, В и С, как из центров, проводим, дуги радиусами, несколько большими половины дуги ВС или АВ. Точки пересечения этих дуг Е и F соединяем с центром окружности О и продолжаем до пересечения с противоположными дугами AD. и DC. При пересечении этих прямых с окружностью получаем точки К, L, М и N. Соединив их последовательно между собой, получим квадрат KLMN, вписанный в окружность, вершины которого разделят окружность на четыре равные части.

Рис. 9. Деление окружности на равные части и вписывание в нее треугольника (а), квадрата (б) и восьмиугольника (в).

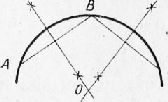
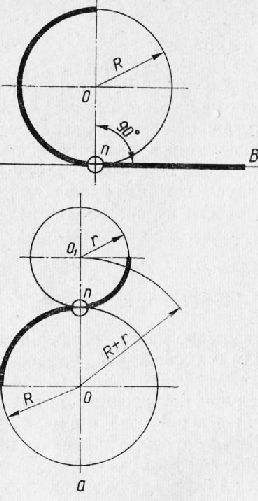
Соединив последовательно точки A, L, В, М, С, N, D, К, А, получим правильный восьмиугольник ALBMCNDK, вершины которого разделят окружность на восемь равных частей.

Нахождение центра окружности или дуги и определение величины радиуса

Найти центр данной дуги.

Намечаем три произвольно расположенные на дуге точки Л, Б и С и соединяем точку А с точкой В, а точку В с точкой С прямыми линиями, которые являются хордами. В середине каждой хорды восстанавливаем перпендикуляр. Точка О пересечения перпендикуляров является искомым центром дуги, а расстояние от точки О до любой точки данной дуги будет величиной радиуса, которым проведена дуга.

Нахождение центра окружности и определение величины ее радиуса производится таким же способом.

Построение сопряжений

Сопряжением называется плавный переход одной линии в другую.

Построение сопряжений основано на свойствах прямой, касающейся окружности, или на свойствах касающихся между собой дуг окружностей.

Рассмотрим два основных случая построения сопряжений.

1. Сопряжение прямой линии с дугой окружности. Для получения плавного перехода от прямой линии к дуге окружности нужно, чтобы центр окружности находился на перпендикуляре к прямой, проведенной в точке касания.

Построение сводится к проведению касательной прямой к окружности в точке п, расположенной на окружности (рис. 27). Проводим окружность с центром в точке О радиусом R, а из точки п восстанавливаем перпендикуляр АВ к отрезку пО. Прямая АВ будет искомой касательной к окружности в точке п. Точка О называется центром сопряжения, R — радиусом сопряжения, п — точкой сопряжения (касания).

Рис. 10. Нахождение центра дуги и определение ее радиуса.

2. Сопряжение двух дуг окружностей. Встречаются два случая сопряжения дуг окружностей: дуги имеют внешнее касание; дуги имеют внутреннее касание.

Плавный переход от одной дуги к другой в этих случаях достигается только тогда, когда точка их касания лежит на прямой линии ООъ соединяющей центры сопрягаемых дуг.

Рис. 11. Сопряжение прямой линии с дугой окружности.

Рис. 12. Сопряжение дуг: а — с внешним касанием; б — с внутренним касанием.

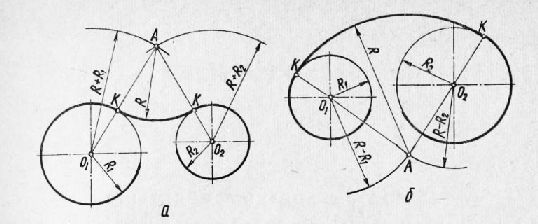
Рис. 13. Сопряжение двух окружностей дугой заданного радиуса: а — внешнее сопряжение; б — внутреннее сопряжение.

При внешнем касании расстояние между центрами 00х равно R + г, т. е. сумме радиусов сопрягаемых дуг. При внутреннем касании это расстояние равно R — г, т. е. разности радиусов сопрягаемых дуг.

Внешнее сопряжение двух окружностей дугой заданного радиуса. При внешнем касании дуги заданного радиуса R двух окружностей центр дуги сопряжения А относительно окружностей радиусов Ri и Rz будет лежать в точке пересечения двух концентрических окружностей, проведенных из центров Ох и 02 радиусами, равными сумме радиусов R + Ri и R + R2 соответственно.

Точки касания К будут лежать на линиях, соединяющих центры 01 ц 02 с точкой А.

Внутреннее сопряжение двух окружностей дугой заданного радиуса. При внутреннем касании дуги заданного радиуса R двух окружностей центр дуги сопряжения А будет лежать в точке пересечения двух концентрических окружностей, проведенных из центров Ох и 02 радиусами, равными разности радиусов R — R1 и R — R2 соответственно.

Точки касания К будут лежать на продолжении прямых, соединяющих точку А с центрами Ох и 02.


Реклама:



Читать далее:



Статьи по теме:


Главная → Справочник → Статьи → Блог → Форум